Biography
I am currently working as a postdoctoral research fellow at the University of Michigan, supervised by Dr. Henry Liu (Download my CV here). I received my Ph.D. degree in Civil Engineering and Scientific Computing at University of Michigan in 2023 and my Bachelor’s degree in School of Vehicle and Mobility at Tsinghua University. My research interests include traffic flow model, traffic control & operations, particularly with big data and connected & automated transportation. My research works are founded on a variety of methodologies including applied statistics, network science, machine learning, and optimization. My work on optimizing traffic signals with connected vehicle data has been covered by media including UofM news, AP news, and Wall Street Journal. I am honored to have received the 2024 INFORMS TSL Best Dissertation Award and to be a finalist for the IEEE ITSS Best Dissertation Award.
- Traffic Flow and Network Model
- Traffic Operation and Control
- Connected and Automated Transportation
PhD in Civil Engineering and Scientific Computing, 2023
University of Michigan
BE in Automotive Engineering, 2018
Tsinghua University
News
- 10/2024: Excited to share that all four of my co-authored papers have been accepted for presentation at this year’s TRB Annual Meeting. Looking forward to the event!
- 10/2024: Our story using connected vehicle data is featured in Roads and Bridges magazine!
- 09/2024: I co-organized the work shop “Vehicle Trajectory Data Camp” at ITSC 2024 at Edmonton. Come and join our discussion! I will serve as the moderator for the second half of this session and am looking foward to meeting you at Edmonton!
- 09/2024: I am incredibly honored to share that my PhD dissertation has been awarded the INFORMS TSL Best Dissertation Award. This award is the oldest and most prestigious recognition for doctoral dissertations in the transportation science and logistics area, and I am deeply humbled to receive it. I will give a talk regarding this during 2024 INFORMS Annual Meeting, looking forward to seeing you in Seattle!
- 08/2024: I am glad to share that my PhD dissertation was selected as the finalist of IEEE ITSS Best Dissertation Award.
Archived News
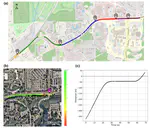
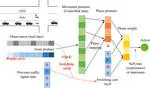
- 06/2024: Our work “Traffic light optimization with low penetration rate vehicle trajectory data” has been featured in The Wall Street Journal! “They use data gathered directly from new, internet-connected vehicles or from navigation apps on their drivers’ phones to help municipalities adjust the timing of their traffic lights, making them more responsive to real-world traffic patterns.”
- 05/2024: Zachary and Zihao presented our work (“Traffic light optimization with low penetration rate vehicle trajectory data”) and earned the first place of the CCAT 2024 student poster competition!
- 02/2024: Our paper “Traffic light optimization with low penetration rate vehicle trajectory data” was recently accepted and is now online in Nature Communications. See the news from University of Michigan, AP News.
- 02/2024: My new personal webiste is online!
- 08/2023: I successfully defended my Dissertation titled “Traffic Signal Optimization with Connected Vehicle Trajectories” advised by Dr. Henry Liu.